
Figure 6
Thereare two typesof pressure:
absolute
and
relative
.
The absolute pressure
is that which includes, in
addition to the pressure that we generate through a
pump, the atmospheric pressure.
Thepressureof theair available tobeusedoutside the
receptacle is defined as
relative pressure
(or gauge
pressure) - i.e. that indicated by the pressure gauge.
Tomeasureatmosphericpressureweuse the
barometer
,
while tomeasure the pressure of a gas enclosed in a
container we use the
manometer (pressure gauge)
.
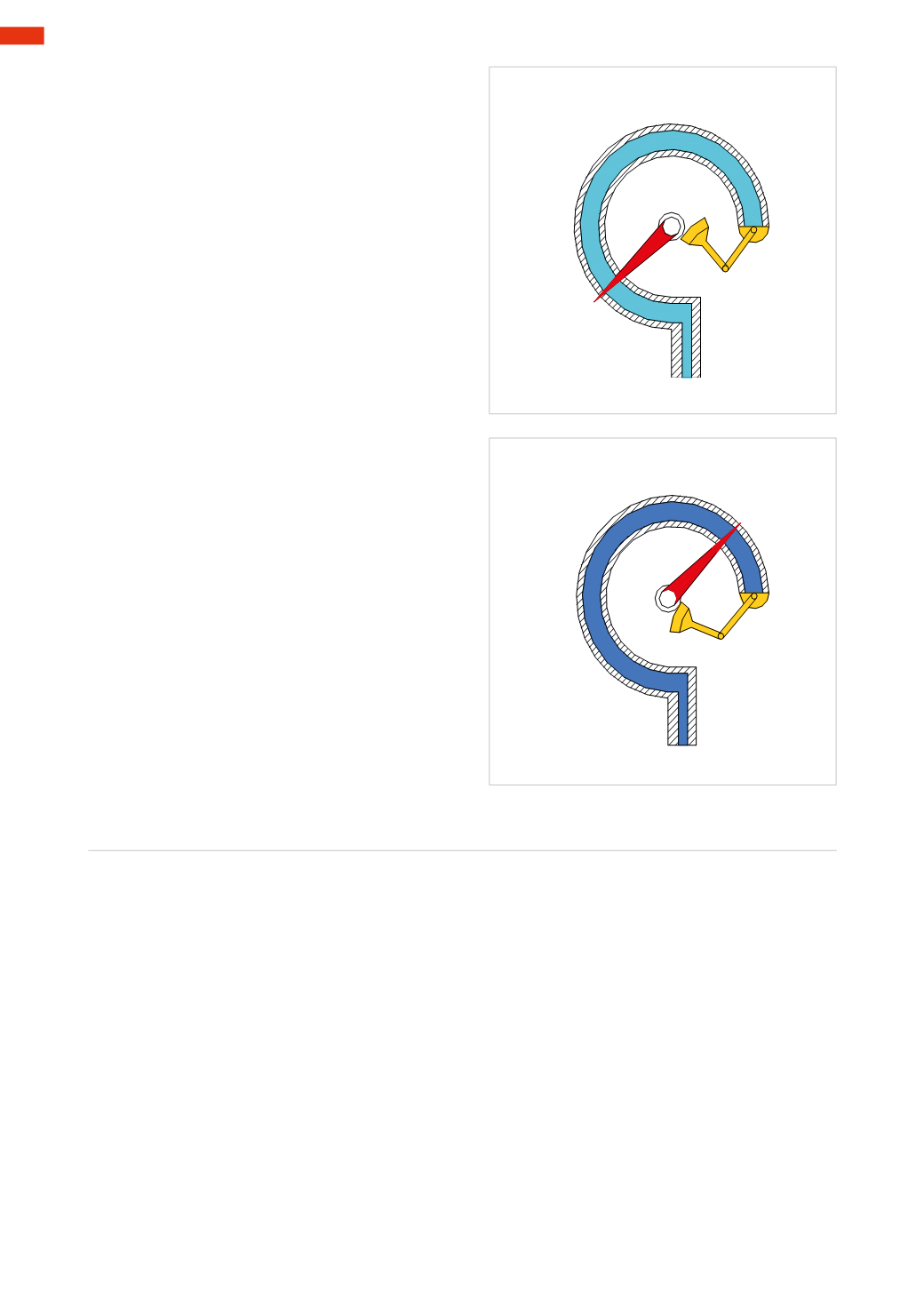
It ismadeof ametallic tube,withanelliptical section,
in the shape of a circumference.
By varying the relative pressure at the end
B
, the
tube varies its length. Point
A
, which is sensitive to
this change, reflects this on the scale as a result of
the rotary motion of a hinge. In this case, the gauge
doesn’t giveus any value since the pressuredifference
between the inside and the outside of the tube is
zero
.
Figure 7
Through this figurewe can observe that, by increasing
thepressureat theend
B
, the
A
end tends tostraighten
andmove the index, as the resistance created by the
external atmospheric pressure is overcome.
Thedifferencebetween the twopressures determines
the angular displacement of the index.
A
1
0
B
3
2
4
Fig. 6
2
4
0
1
3
Fig. 7
Boyle’s law
The state of a gas is described through three parameters:
Volume
,
Pressure
, and
Temperature
.
To understand the relationship between them, we study how a gas behaves by controlling one of these parameters
and observing the behaviour of the others. A particular characteristic of gas is its capacity to expand and occupy
the largest volume available. With the following examples, we study the change of pressure and volume at a
constant temperature.
Figure 8
Pos. 1
: a rigid transparent tubewith a constant section andwith a
U
shape is arranged in a vertical positionwith
the long arm exposed and the short arm connected to a tap. Filling themercury tube, the height of themercury in
the twoarmswill beequal, since theatmospheric pressure is actingonboth surfaces.We close the tap, the volume
of air present in the shorter arm, (subject to the atmospheric pressure) is denoted by
V
X
, with
x
as its height.
Pos. 2
: we pour additional mercury through the open armwhereby the volume of the air in the short arm halves.
We observe a difference in the level of mercury in the two arms of 76
cm
, i.e. 1
bar
.
Pos. 3
: continuing to add mercury, we observe that when the volume of the trapped air becomes a third of the
initial value, the difference in levels is 76
cm
+ 76
cm
= 152
cm
, i.e. 2
bar
.
1
16
CAMOZZI
>
PHYSICS

















