
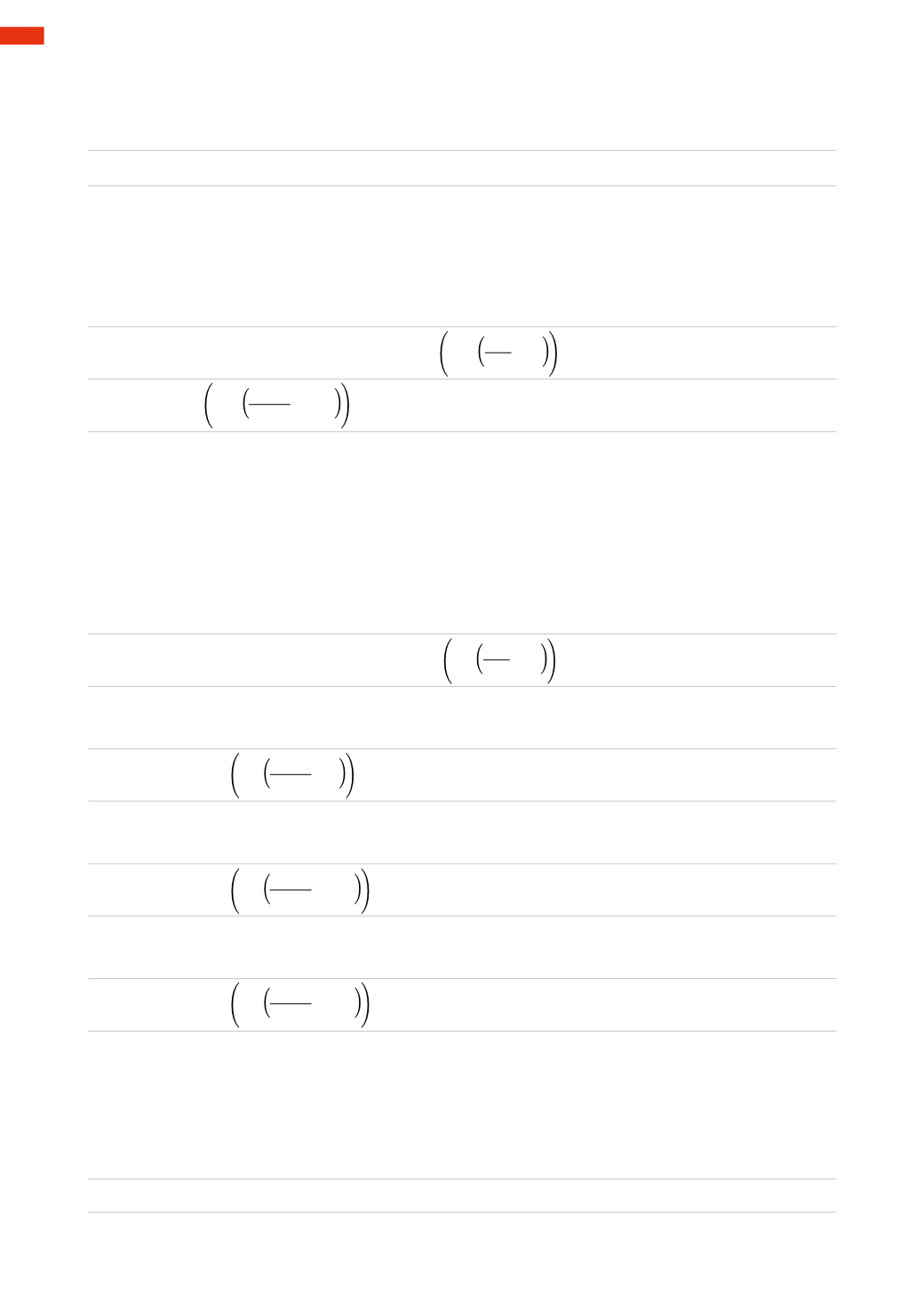
The second law of Gay-Lussac states that:
at constant volume the pressure of a gas increases linearly with temperature.
The formula for the calculation of pressurewhen
V
=
K
(constant) is:
p
t
=
p
0
* (
1+
α
t)
p
t
is the pressure at
t °C
p
0
is the pressure at
0 °C
t
is the temperature in
°C
Increasing the temperature of a gas from 0
°C
to 100
°C
, the pressure becomes:
p
t
=
p
0
*
1+ 1
t
1
*
∆
t
p
t
=
p
0
*
1+ 1
273 * 100
p
t
=
p
0
*
�
1+
�
0,0036
* 100
��
p
t
=
p
0
*
1,36
dm
3
the pressure of the gas increases by about 36%.
If the temperature is reduced to values lower than 0
°C
, the pressure
p
t
is proportionally reduced to zero at a
temperature of –273
°C
. At this temperature, defined as absolute zero, all gases are now in the liquid state.
In fact most gases liquefy before reaching this temperature, nitrogen at –196
°C
,hydrogen at –253
°C
, helium at
–269
°C
.
In the case of a temperature reduction the previous formula changes slightly:
p
t
=
p
0
*
1 – 1
t
1
*
∆
t
Example:
the initial pressure is 10
bar
, if it causes a decrease of temperature of 1
°C
, the pressure becomes:
p
t
=
p
0
*
1 – 1
273 * 1
p
t
=10
*
�
1 –0,0036
�
p
t
=
9,96
bar
for a reduction of 100
°C
, the pressure is reduced to a value of:
p
t
=
p
0
*
1 – 1
273 * 100
p
t
=10
*
�
1 –0,36
�
p
t
=
6,33
bar
for a reduction of 273
°C
, the pressure is reduced to a value of:
p
t
=
p
0
*
1 – 1
273 * 273
p
t
=10
*
�
1 –1
�
p
t
=
0
bar
at a temperature of –273
°C
the pressure becomes 0.
The unit of measure commonly used for temperature is the degree Celsius (
°C
) and relates to a temperature
scale that registers the freezing point of water as 0
°C
and the boiling point as 100
°C
under normal atmospheric
pressure. The unit of measurement used in the International System is the degree kelvin, which has a value equal
to that of 1 degree Celsius, even if the scale is different.
0
°C
=
273
K
100
°C
=
373
K
1
20
CAMOZZI
>
PHYSICS

















