
KATALOG >
Version 8.8
ANHANG >
Technische Produktinformationen
a
ANHANG
Berechnung:
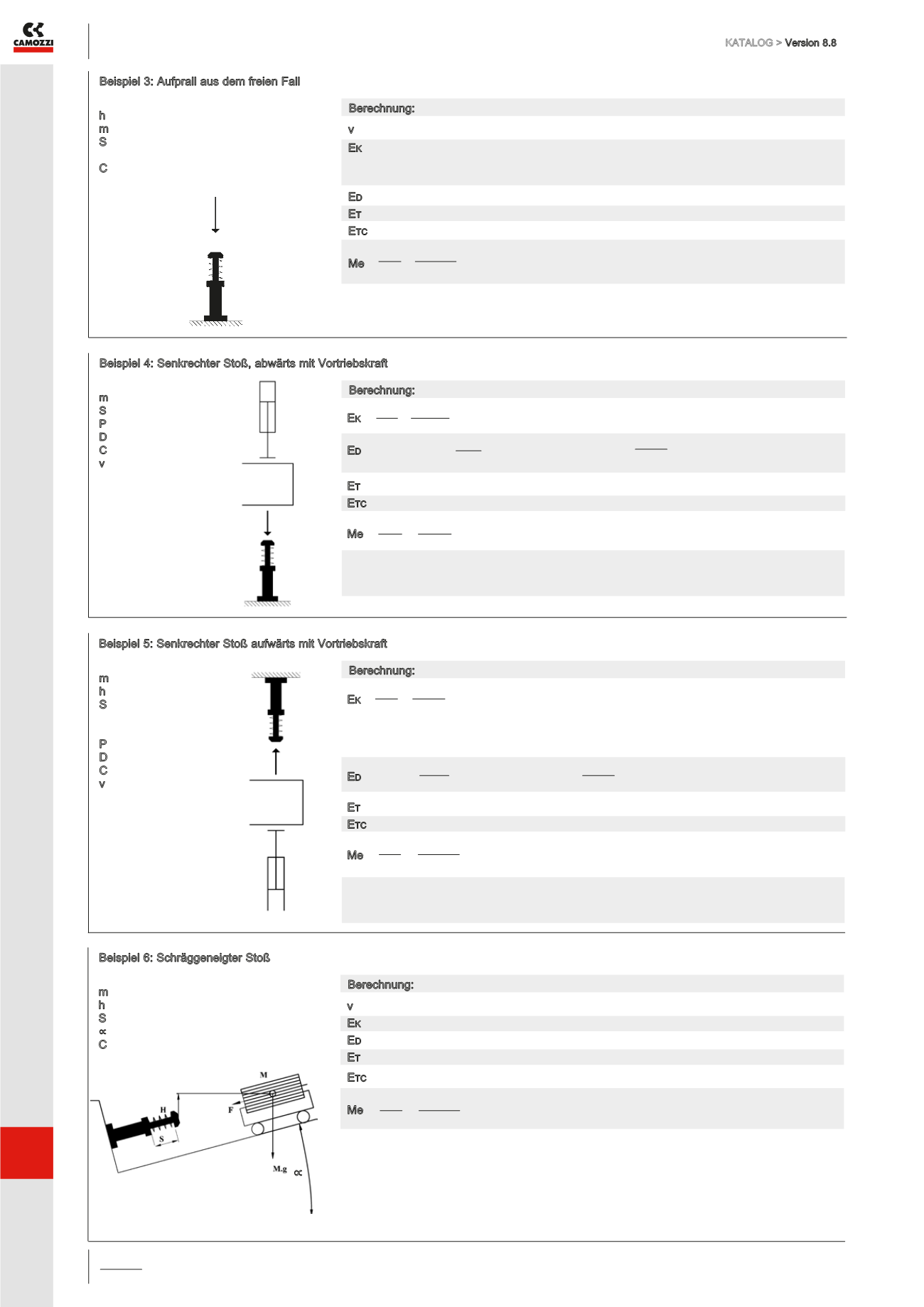
Beispiel 3: Aufprall aus dem freien Fall
Anwendungsdaten:
h = 0,35 m
m = 5 kg
S = 0.01 m
erste Hypothese Mod. SA 1210
C = 1500 Zyklen/h
v = √ (2g . h) √ (2 . 9,81 . 0,35) = 2,6 m/s
E
k
= m . g . h = 5 . 9,81 . 0,35 = 17,2 Nm
Bei einem Stoßdämpfer mit dem niedrigsten Et, aber mit dem höchsten Wert der
kinetischen Energie von 17.2 Nm entspricht dies dem Mod. SA 1412 mit S=0.012 m
E
d
= F . S = m . g . s = 5 . 9,81 . 0,012 = 0,6 Nm
E
t
= E
k
+ E
d
= 17,2 + 0,6 = 17,8 Nm
E
tc
= E
t
. C = 17,8 . 1500 = 26700 Nm/h
Me = 2E
t
= 2 . 17,5 = 5 Kg
v
2
2,6
2
Berechnung:
Beispiel 4: Senkrechter Stoß, abwärts mit Vortriebskraft
Der in diesem Fall geeignete Stoßdämpfer ist der SA 2725, gemäß den technischen Daten, in
denen wir finden, dass Et (max)=147 Nm, Etc (max)=72000 Nm/h und Me(max)=270 kg ist.
Der in diesem Fall geeignete Stoßdämpfer ist der SA 1412, gemäß den technischen Daten,
in denen wir finden, dass Et (max)=20 Nm, Etc (max)=33000 Nm/h und Me(max)=40 kg ist.
Anwendungsdaten:
m = 50 kg
S = 0.025 m
P = 6 bar
D = 63 mm
C = 600 Zyklen/h
v = 1,0 m/s
Berechnung:
Beispiel 5: Senkrechter Stoß aufwärts mit Vortriebskraft
Anwendungsdaten:
m = 50 kg
h = 0.3 m
S = 0.025 m
erste Hypothese
Mod. SA 2525
P = 6 bar = 0,6 MPa
D = 63 mm
C = 600 Zyklen/h
v = 1,0 m/s
E
k
= mv
2
= 50 . 1
2
= 25 Nm
2 2
Bei einem Stoßdämpfer mit dem niedrigsten Et, aber mit dem höchsten Wert der kinetischen
Energie von 25 Nm entspricht dies dem Mod. SA 2015 mit S=0.015 m
E
d
= F . S = ( D
2
.
π
. P . g/100 – m . g) . S = ( 63
2
.
π
6 . 9,81/100 – 50 . 9,81) . 0,015 = 20,1 Nm
4
4
E
t
= E
k
+ E
d
= 25 + 20,1 = 45,7 Nm
E
tc
= E
t
. C = 45,1 . 600 = 27060 Nm/h
Me = 2
E
t
= 2 . 45,7 = 91,4 Kg
v
2
1
2
E
k
= mv
2
= 50 . 1
2
= 25 Nm
2 2
E
d
= F . S = (m . g + D
2
.
π
. P . g/100 ) . S = (50 . 9,81 + 63 .
π
. 6 . 9,81/100) . 0,025 = 58,1 Nm
4
4
E
t
= E
k
+ E
d
= 25 + 58,1 = 83,1 Nm
E
tc
= E
t
. C = 83,1 . 600 = 49860 Nm/h
Me = 2
E
t
= 2 . 84 = 168 Kg
v
2
1
2
Der in diesem Fall geeignete Stoßdämpfer ist der SA 2015, gemäß den technischen Daten, in
denen wir finden, dass Et (max)=59 Nm, Etc (max)=38000 Nm/h und Me(max)=120 kg ist.
Berechnung:
Beispiel 6: Schräggeneigter Stoß
Anwendungsdaten:
m = 10 kg
h = 0,3 m
S = 0.015 m
∝
= 30°
C = 600 Zyklen/h
v = √ (2g . h) √ (2 . 9,81 . 0,3) = 2,43 m/s
E
k
= m . g . h 10 . 9,81 . 0,3 = 29,4 Nm
E
d
= F . S = m . g . sin
α
. s = 10 . 9,81 . sin30° . 0,015 = 10 . 9,81 . 0,5 . 0,015 = 0,7 Nm
E
t
= E
k
+ E
d
= 29,4 + 0,7 = 30,1 Nm
E
tc
= E
t
. C = 30,1 . 600 = 18060 Nm/h
Me = 2
E
t
= 2 . 30,1 = 10,2 Kg
v
2
2,43
2a
Der in diesem Fall geeignete Stoßdämpfer ist der SA 2015, gemäß den technischen Daten, in
denen wir finden, dass Et (max)=59 Nm, Etc (max)=38000 Nm/h und Me(max)=120 kg ist.
∝
a
/3.05



















